树（Tree）

李艳生

湖北师范大学

物理与电子科学学院

2020年春季

回顾

• 非线性数据结构
  • 数组（随机访问）
  • 栈（后进先出）
  • 队列（先进先出）
  • 链表（增删方便）
  • 集合（不重复性）
  • 字典（键值对）
  • 散列表（查找高效）

引入

家谱

引入

目录

引入

菜单

树的概念

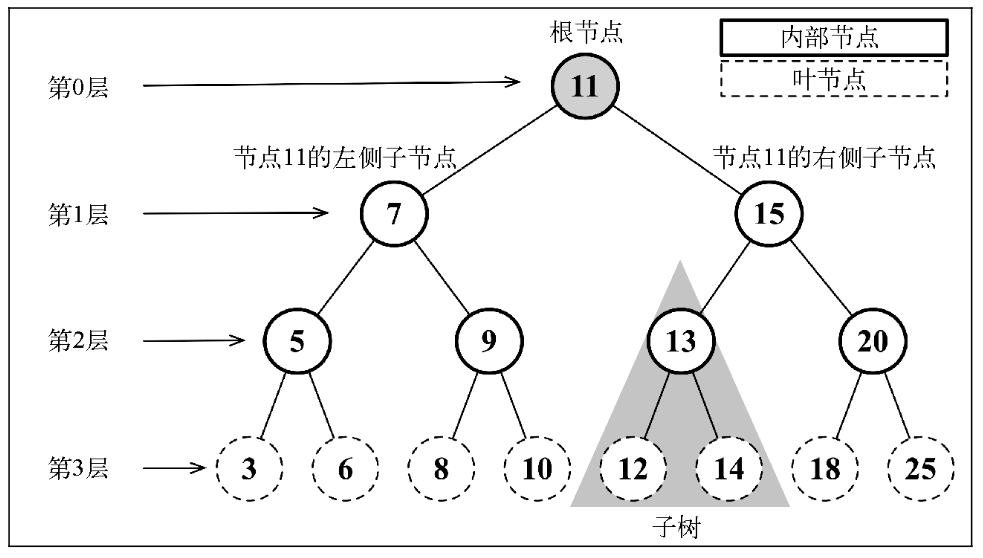
树的概念

• 树：包含一系列父子关系的节点。
• 节点：只有一个父节点和0个或多个子节点
• 根节点：没有父节点
• 叶子节点：没有子节点
• 子树：由节点和它的子孙节点组成
• 节点的深度：祖先节点的个数
• 树的高度：所有节点深度的最大值

二叉树

• 二叉树Binary Tree
  • 每个节点最多只有两个子节点
  • 即左子节点和右子节点

二叉搜索树

• 二叉搜索树Binary Search Tree
  • 左节点存储比它小的值
  • 右节点存储比它大的值

二叉搜索树操作

• 创建
• 插入
• 查找
• 删除
• 遍历
• 找最大值、最小值

创建

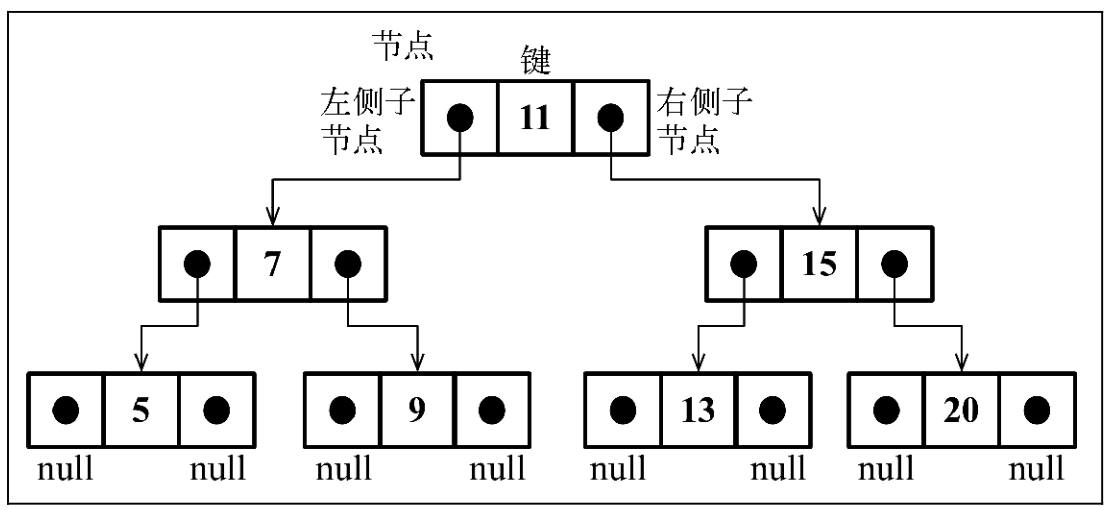
创建节点

• 存储节点值，并要指向左子节点和右子节点

class Node {   
    constructor(key) {     
        this.key = key; // 节点值    
        this.left = null; // 指向左子节点    
        this.right = null; // 指向右子节点  
    } 
}

创建树

• 链表创建头结点对象，头结点head属性指向链表第一个节点
• 树创建一个对象,对象root属性指向树的根节点

创建树

function defaultCompare(a, b) {
  if (a === b) {
    return 0;
  }
  return a < b ? -1 : 1;
}

class BinarySearchTree {
    constructor(compareFn = defaultCompare) {     
        this.compareFn = compareFn; // 用来比较节点值    
        this.root = null; //  指向Node类型的根节点  
    }
    insert(key){}
    search(key){}
    remove(key){}
    inOrderTraverse(){}
    preOrderTraverse(){}
    postOrderTraverse(){}
    min(){}
    max(){} 
} 

插入

• 第一步是如果树为空，即root为null,创建一个根节点，并用root指向它。
• 第二步是将节点添加到根节点以外的其他位置。

插入

insert(key) {
  if (this.root == null) { //树为空
    this.root = new Node(key); //插入根节点
  } else {
    this.insertNode(this.root, key); //插入其它位置
  }
}
insertNode(node, key) {
  if (this.compareFn(key, node.key) === -1) { //key < node.key
    if (node.left == null) {
      node.left = new Node(key);
    } else {
      this.insertNode(node.left, key); //递归插入左子树
    }
  } else if (node.right == null) { //node右子节点为空
    node.right = new Node(key); //插入右子节点位置
  } else {
    this.insertNode(node.right, key); //递归插入右子树
  }
}

插入使用

//创建一个树对象
const tree = new BinarySearchTree(); 
//插入一个值
tree.insert(7); 
tree.insert(15); 
tree.insert(5); 
tree.insert(3); 
tree.insert(9); 
tree.insert(8); 
tree.insert(10); 
tree.insert(13); 
tree.insert(12); 
tree.insert(14); 
tree.insert(20); 
tree.insert(18); 
tree.insert(25);
tree.insert(6)

插入使用

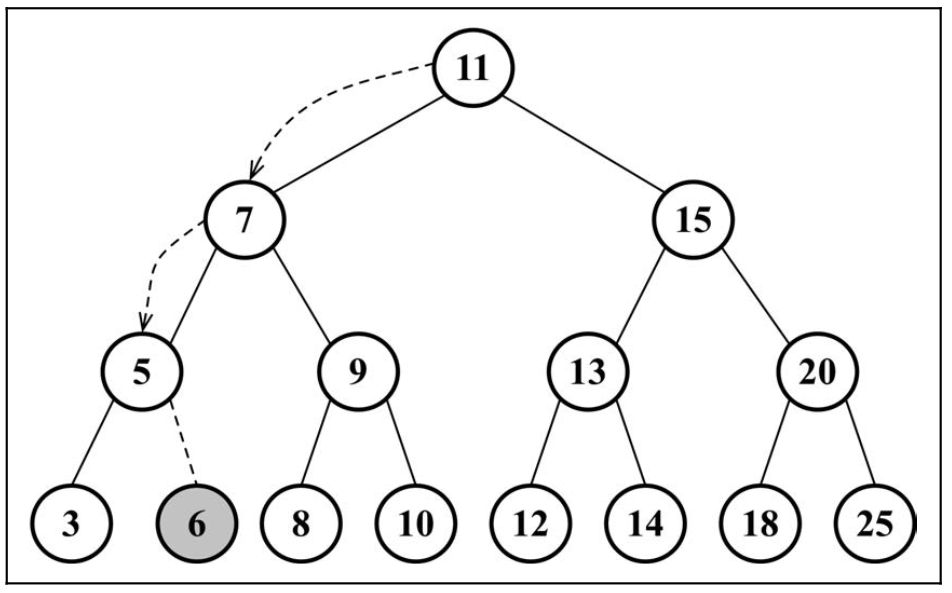
树的遍历

遍历一棵树是指访问树的每个节点并对它们进行某种操作的过程

中序遍历
先序遍历
后序遍历

中序遍历

• 左子节点--节点--右子节点，即从小到大顺序访问

inOrderTraverse(callback) {
  this.inOrderTraverseNode(this.root, callback);
}

inOrderTraverseNode(node, callback) {
  if (node != null) {
    this.inOrderTraverseNode(node.left, callback); //递归左子节点
    callback(node.key); //访问节点
    this.inOrderTraverseNode(node.right, callback); //递归右子节点
  }
}

中序遍历的使用

//定义一个访问函数
const printNode = (value) => console.log(value); 
//中序遍历
tree.inOrderTraverse(printNode);

中序遍历的使用

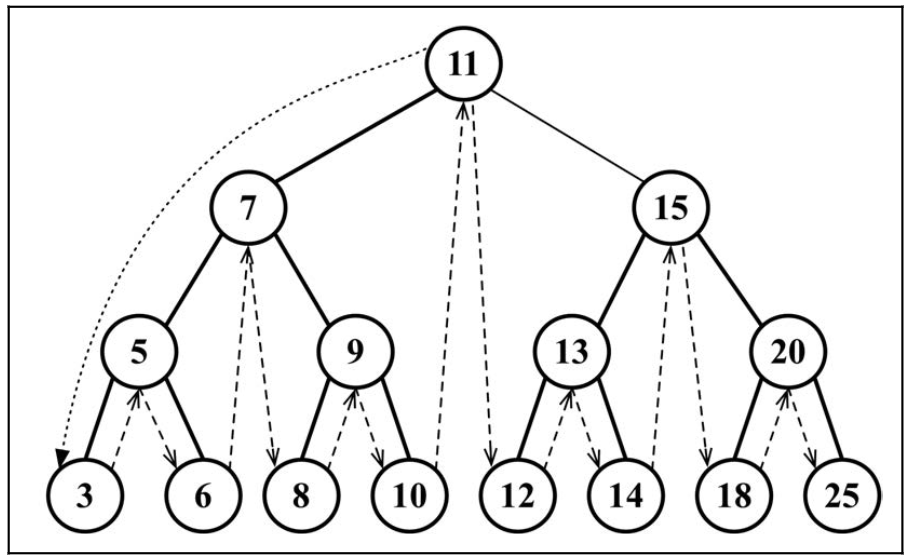
先序遍历

• 节点--左子节点--右子节点，即优先后代节点访问

preOrderTraverse(callback) {
  this.preOrderTraverseNode(this.root, callback);
}
preOrderTraverseNode(node, callback) {
  if (node != null) {
    callback(node.key); //访问节点
    this.preOrderTraverseNode(node.left, callback);//递归左子节点
    this.preOrderTraverseNode(node.right, callback);//递归右子节点
  }
}

先序遍历的使用

//定义一个访问函数
const printNode = (value) => console.log(value); 
//先序遍历
tree.preOrderTraverse(printNode);

先序遍历的使用

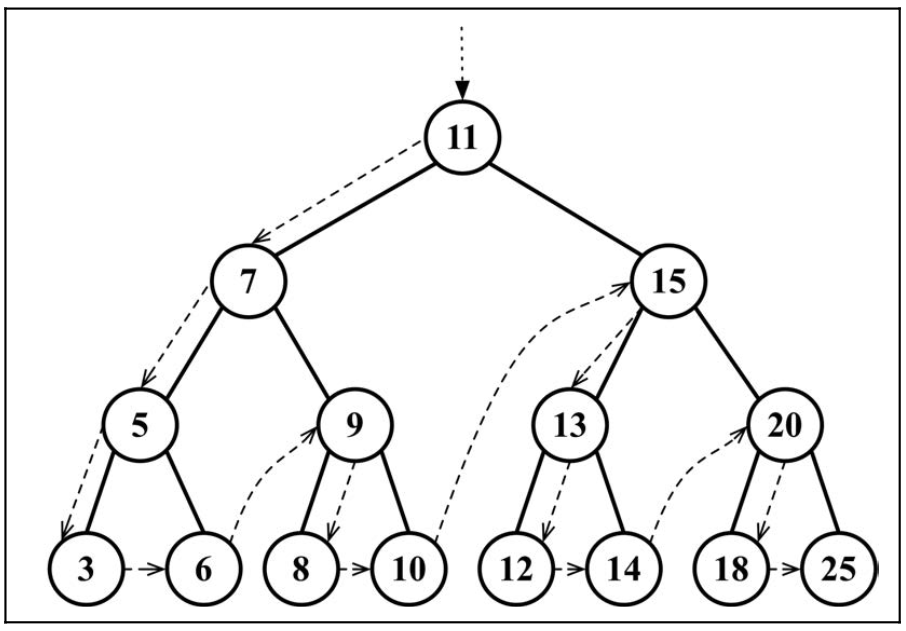
后序遍历

• 左子节点--右子节点--节点，即优先访问后代节点

postOrderTraverse(callback) {
  this.postOrderTraverseNode(this.root, callback);
}
postOrderTraverseNode(node, callback) {
  if (node != null) {
    this.postOrderTraverseNode(node.left, callback);//递归左子节点
    this.postOrderTraverseNode(node.right, callback);//递归右子节点
    callback(node.key); //访问节点
  }
}

后序遍历的使用

//定义一个访问函数
const printNode = (value) => console.log(value); 
//先序遍历
tree.preOrderTraverse(printNode);

后序遍历的使用

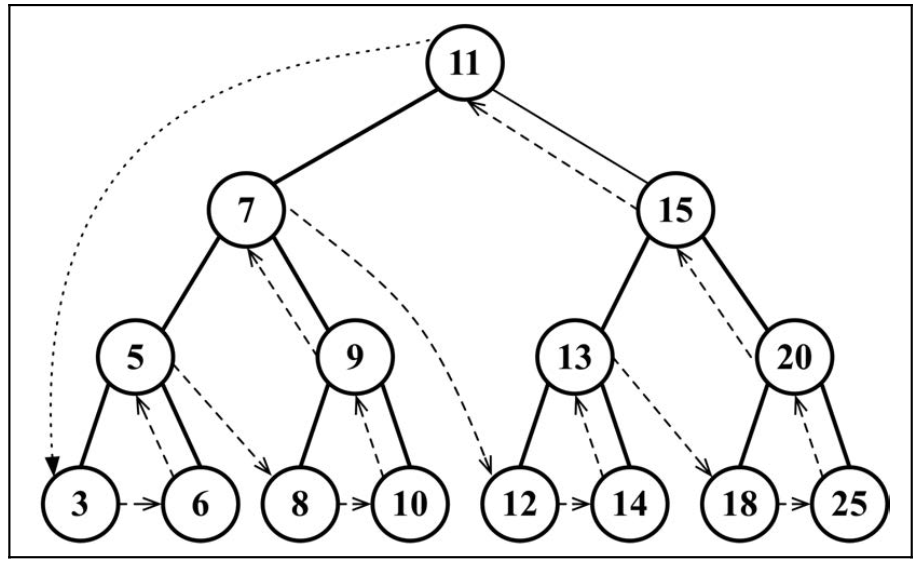
搜索最大值最小值

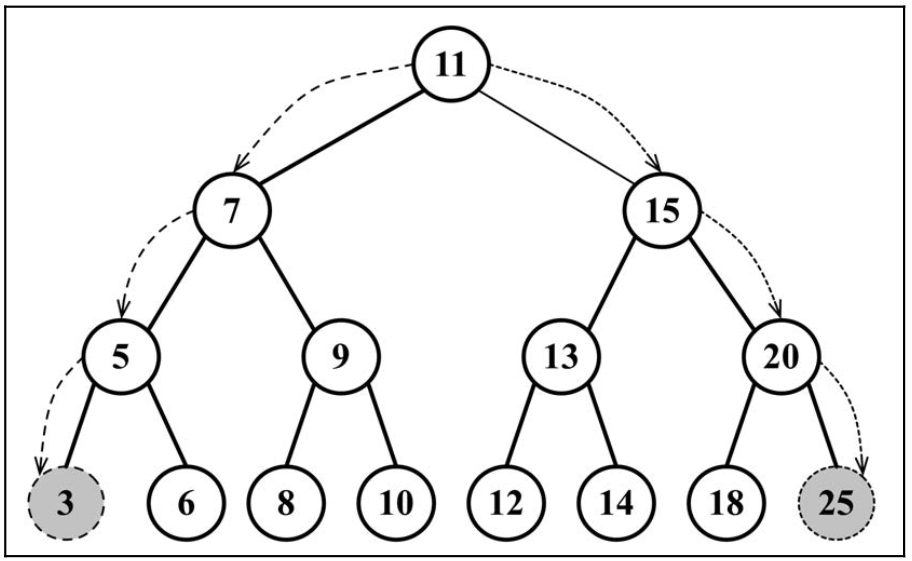
搜索最小值

• 找最左边的叶子节点即为最小值

min() {
  return this.minNode(this.root);
}
minNode(node) {
  let current = node;
  //找最左边的叶子节点
  while (current != null && current.left != null) {
    current = current.left;
  }
  return current;
}

搜索最大值

• 找最右边的叶子节点即为最小值

max() {
  return this.minNode(this.root);
}
maxNode(node) {
  let current = node;
  //找最左边的叶子节点
  while (current != null && current.right != null) {
    current = current.right;
  }
  return current;
}

搜索特定值

search(key) {
  return this.searchNode(this.root, key);
}

searchNode(node, key) {
  if (node == null) {
    return false;
  }
  if (this.compareFn(key, node.key) === -1) { //key < node.key
    return this.searchNode(node.left, key); //搜索左子树
  } if (this.compareFn(key, node.key) === 1) { //key > node.key
    return this.searchNode(node.right, key); //搜索右子树
  }
  return true;
}

删除

• 第一步，找到要删除的节点
• 第二步，删除该节点，分三种情况
  • 该节点为叶子节点时，node = null,直接删除即可
  • 该节点只有一个子节点时，父节点指向子节点即可
  • 该节点有两个子节点时，分三步
    • 第一步找到该节点右子树上最小值节点
    • 第二步将最小值节点值赋给该节点
    • 第三步删除该节点右子树上最小值节点

删除叶节点

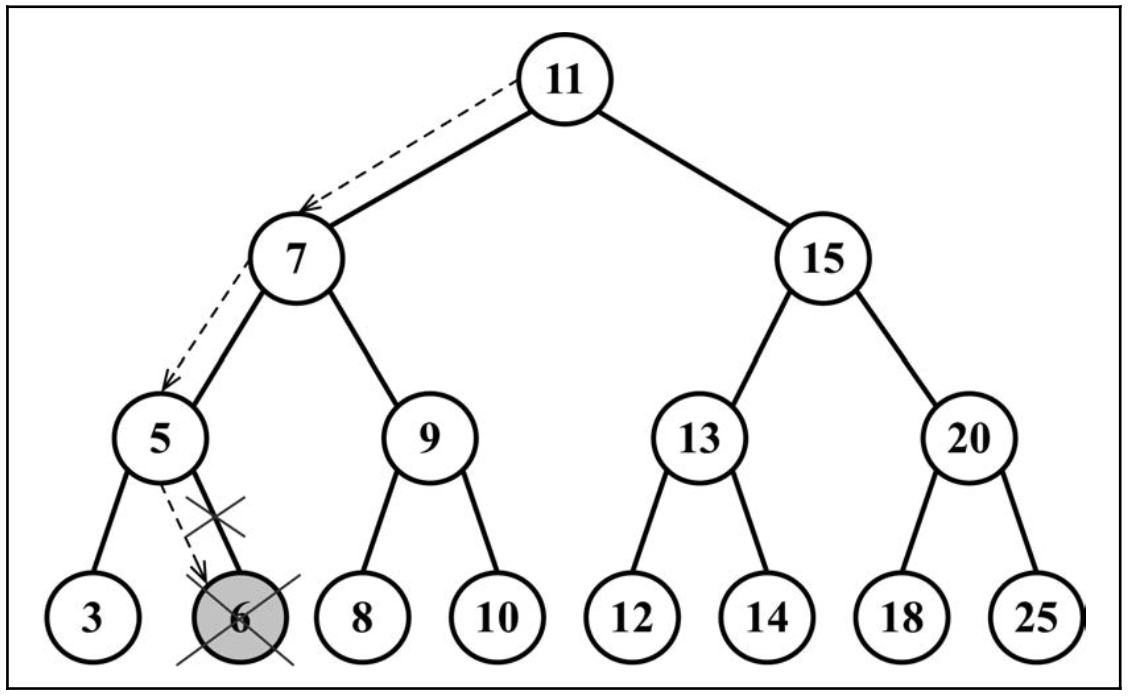
只有一个子节点

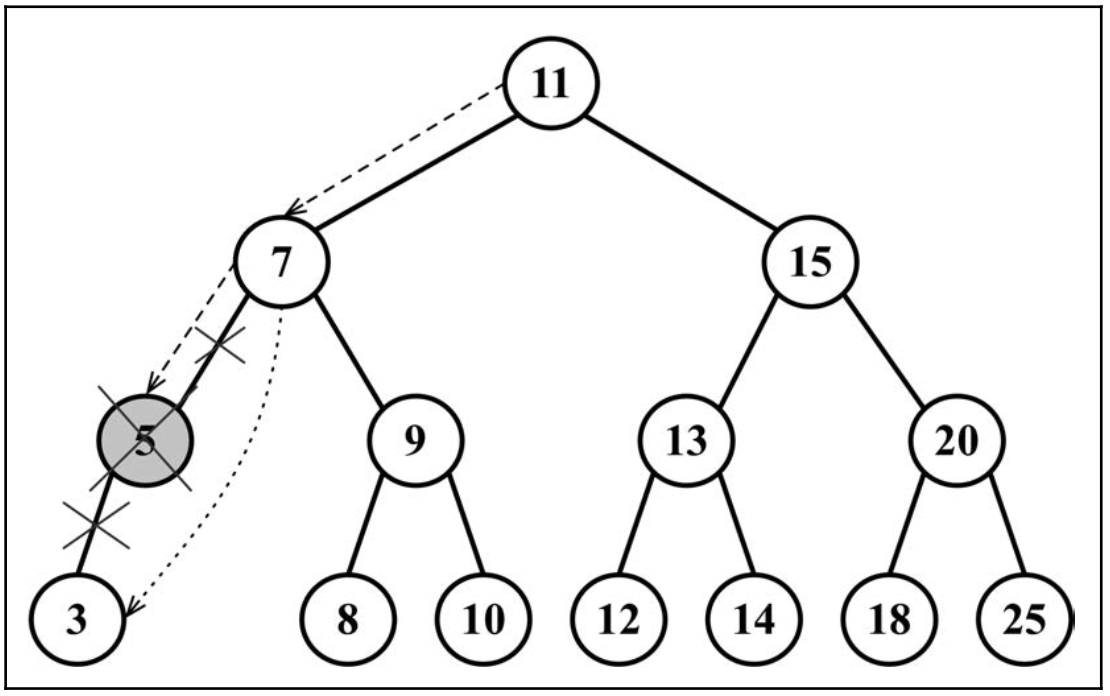
有两个子节点

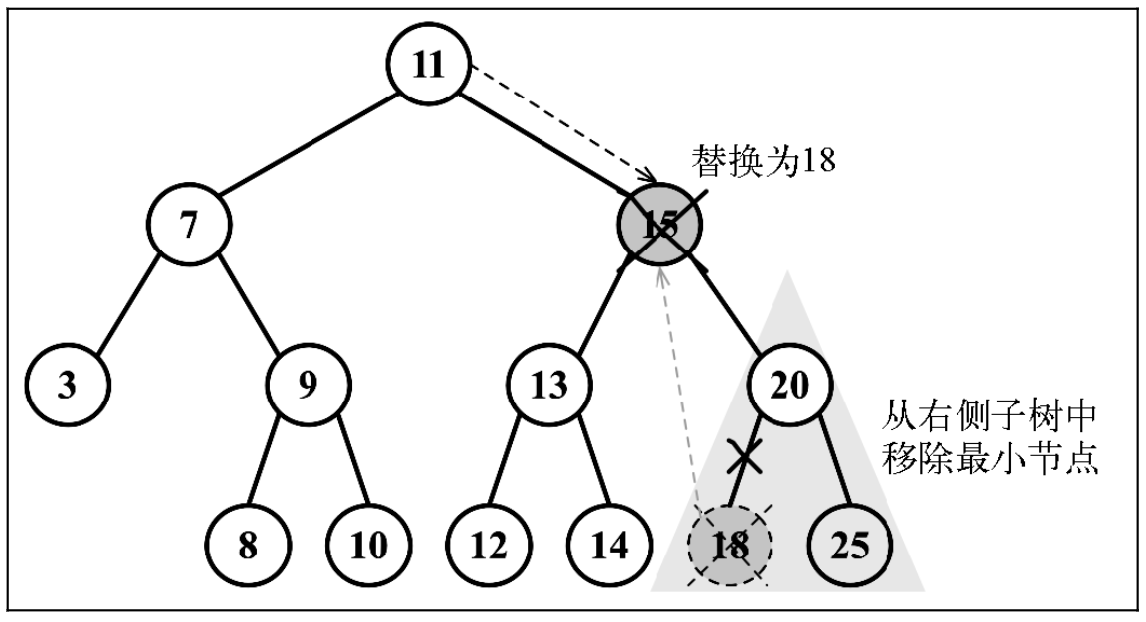
删除

remove(key) {
    this.root = this.removeNode(this.root, key);
}
removeNode(node, key) {
    //没找到
    if (node == null) {
        return undefined;
    }
    //查找节点
    if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
        node.left = this.removeNode(node.left, key);
        return node;
    } if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) {
        node.right = this.removeNode(node.right, key);
        return node;
    }
    // 删除该节点
    // 叶子节点
    if (node.left == null && node.right == null) {
        node = undefined;
        return node;
    }
    // 只有一个子节点
    if (node.left == null) {
        node = node.right;
        return node;
    } if (node.right == null) {
        node = node.left;
        return node;
    }
    // 有两个子节点
    const aux = this.minNode(node.right);
    node.key = aux.key;
    node.right = this.removeNode(node.right, aux.key);
    return node;
}

任务

设计一个二叉搜索树，向树中插入1,2,3,4,5,6,7,8,9,10,分别用先序、中序、后序方式遍历该树。